编程判断素数的代码

素数（质数）指的是只能被1和自身整除的正整数，例如2、3、5、7、11等。在编程中，判断一个数是否为素数是一个常见的问题，通常有以下几种方法：

暴力法： 从2开始，依次尝试将要判断的数除以小于它的所有正整数，如果能整除则该数不是素数。这种方法简单直接，但是效率较低，特别是对于大数。

优化暴力法： 在上一种暴力法的基础上，其实只需要判断从2到该数的平方根之间的数即可，因为大于该数平方根的数如果能整除该数，必定有一个因子小于该数的平方根。

埃氏筛法： 埃氏筛法是一种用来查找一定范围内所有素数的算法。基本思想是从2开始，将每个素数的各个倍数标记为合数。在进行标记的过程中，如果一个数已经被标记为合数，则跳过，因为它必定有更小的素因子已经标记过了。

欧拉筛法： 欧拉筛法是一种改进的埃氏筛法，对于一个数，只用它最小的质因数去筛，从而降低了时间复杂度。

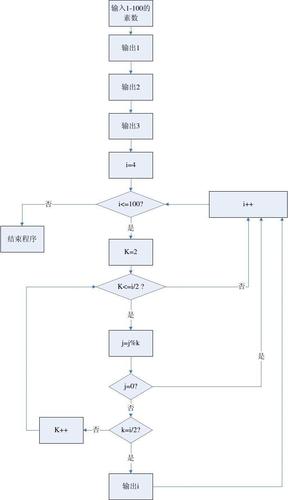
在实际编程中，应选择最适合具体情况的算法。若只是判断个别小数是否为素数，暴力法已经足够；若需要频繁进行素数判断，可以选择埃氏筛法或欧拉筛法来提高效率。

免责声明：本网站部分内容由用户自行上传，若侵犯了您的权益，请联系我们处理，谢谢！联系QQ：2760375052 沪ICP备2023024866号-10